RNN에 기반한 언어 모델은 크게 2가지 문제가있다.
1. 하나의 고정된 크기 벡터에 모든 정보를 압축하려고 하니 정보 손실이 발생
2. RNN의 고질적인 문제인 기울기 소실(Vanishing Gradient) 문제 존재
이를 해결하기 위해 등장한 기법이 바로 어텐션(attention)!
어텐션 기본 아이디어는 디코더에서 출력 단어를 예측하는 매 시점 마다, 인코더에서의 전체 입력 문장을 다시 한 번 참고하는 것이다.주목할 점은 모든것을 동일한 비율로 참고하는 것이 아니라, 해당 시점에서 예측해야 할 단어와 '연관성 있는 부분을 더 집중'하게 된다.
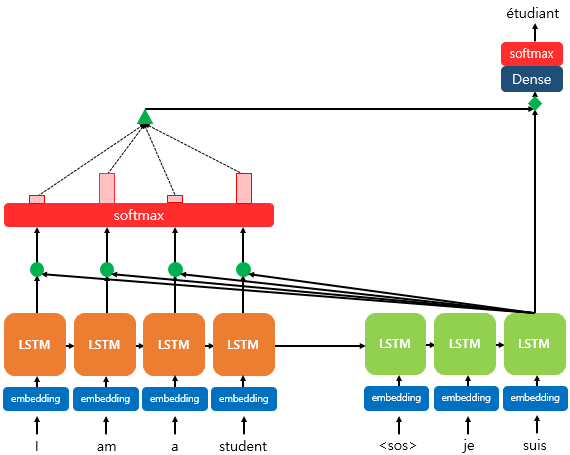
소프트 맥스층을 거쳐 나온 붉은 막대는 출력 단어를 예측할 때 얼마나 도움이 되는지 정도를 나타낸것.
해당 수치는 하나의 정보로 디코더에 전송된다.
결과적으로 디코더가 출력 단어를 더 정확하게 예측할 확률이 높아지게 된다.
1) 어텐션 스코어(Attention Score) 구하기
아래 그림을 보면 각 입력 단어의 은닉 상태와 디코더의 현재 시점 t에서의 은닉 상태 간 내적(dot product)을 수행한다.
주황색 박스로 된 가 인코더의 은닉 상태고, 초록색 박스로 된 가 디코더의 은닉 상태를 가리킨다.
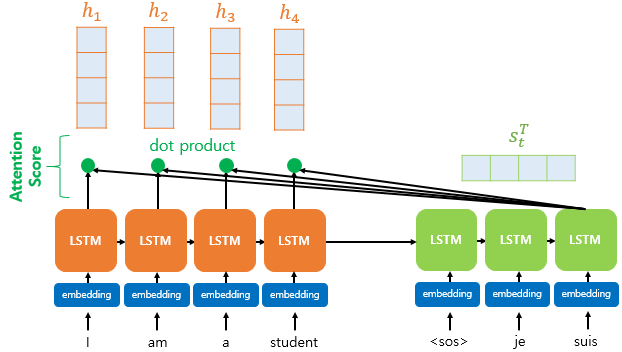
기존의 디코더는 현재 시점 t에서 2개의 입력값을 필요로 했습니다. 하나는 이전 시점 t-1의 은닉 상태와 다른 하나는 이전 시점 t-1에서 나온 출력 단어다. 하지만 어텐션 메커니즘에선 어텐션 값(Attention Value)이라는 새로운 값을 추가로 필요로 한다.
어텐션 스코어란 현재 디코더 시점 t에서 단어를 예측하기 위해, 인코더의 모든 은닉 상태 각각이 디코더의 현 시점 은닉 상태 st와 얼마나 유사한지를 판단하는 스코어값이다.
어텐션 스코어에는 대표적으로 닷-프로덕트(dot-product) 어텐션과 바다나우 어텐션(Bahdanau Attention)이 있다.
닷-프로덕트 어텐션
어텐션 함수
Attention(Q, K, V) = Attention Value
Q = Query : t 시점의 디코더 셀에서의 은닉 상태
K = Keys : 모든 시점의 인코더 셀의 은닉 상태들
V = Values : 모든 시점의 인코더 셀의 은닉 상태들
1. 쿼리에 대해 모든 키와의 유사도를 구함
2. 해당 유사도를 키와 매핑되어 있는 각각의 값(value)에 반영
3. 이렇게 유사도가 반영된 값을 모두 더해 리턴(Attention Value)
디코더 은닉 상태인 st를 전치(transpose)하고 각 은닉 상태와 내적(dot-product)을 수행한다. 예를 들어, st와 인코더의 i번째 은닉 상태의 어텐션 스코어 계산 모습은 아래와 같다.
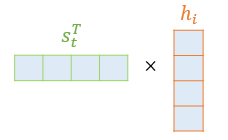
어텐션 스코어 함수 식은 아래와 같다.
score(st,hi)=stThN
와 인코더의 모든 은닉 상태의 어텐션 스코어 모음값을 라고 정의하면 수식은 다음과 같다.
et=[stTh1,...,stThN]
여기서 N은 입력 단어 갯수, 위에선 "I am a student"로 총 4개
위에서 구한 et에 소프트맥스 함수를 적용하면 모든 값을 합했을 때 1이 되는 확률 분포를 얻게 된다. 이를 어텐션 분포라 하며, 각각의 값은 어텐션 가중치(Attention Weight)라고 한다.
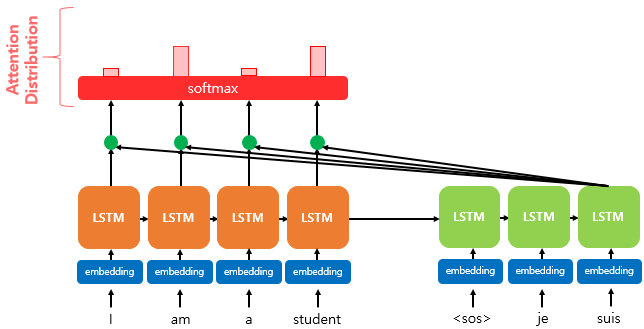
디코더 시점 t에서의 어텐션 가중치 모음값인 어텐션 분포를 라고 할 때, 아래와 같이 표현할 수 있다.
바다나우 어텐션
아래 어텐션 함수는 대체적으로 동일하되 다른 점이 하나 있다.
바로 Query가 디코더 셀의 t 시점의 은닉 상태가 아닌 t-1 시점의 은닉 상태라는 것
어텐션 함수
Attention(Q, K, V) = Attention Value
t = 어텐션 메커니즘이 수행되는 디코더 셀의 현재 시점을 의미.
Q = Query : t-1 시점의 디코더 셀에서의 은닉 상태
K = Keys : 모든 시점의 인코더 셀의 은닉 상태들
V = Values : 모든 시점의 인코더 셀의 은닉 상태들
2) 어텐션 분포(Attention Distribution) 구하기
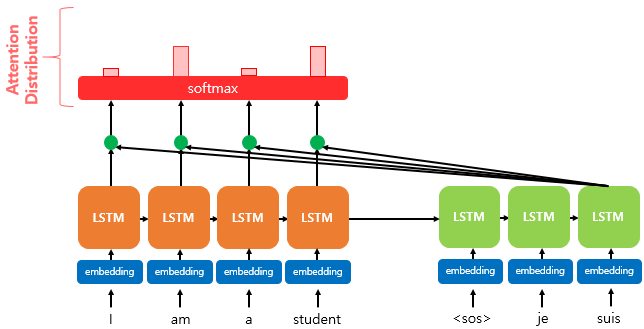
위에서 구한 et에 소프트맥스 함수를 적용하면 모든 값을 합했을 때 1이 되는 확률 분포를 얻게 된다.
이를 어텐션 분포라 하며, 각각의 값은 어텐션 가중치(Attention Weight)라고 한다.
위 그림에서 붉은색 사각형의 크기가 가중치 크기를 나타내고 있다. 크기로 보면 "am", "student"가 동일한 가중치를 가지고 있음을 알 수 있다.
디코더 시점 t에서의 어텐션 가중치 모음값인 어텐션 분포를 αt라고 할 때, 아래와 같이 표현할 수 있다.
3) 어텐션 값(Attention Value) 구하기

이제 어텐션의 최종 결과값을 얻기 위해 각 인코더의 은닉 상태와 어텐션 가중치값들을 곱하고 모두 더해 나오는 값이 어텐션 값이 되며 이를 라고 한다.
at=∑i=1Nαithi
어텐션 값은 인코더의 문맥을 담고 있다고 해서 컨텍스트 벡터(context vector)라고도 불린다.
4) 어텐션 값과 디코더 t 시점의 은닉 상태 연결(Concatenate)
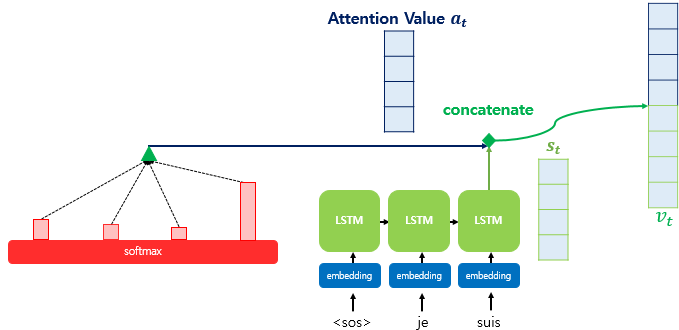
어텐션 값이 구해지면 at를 st와 결합(concatenate)하여 하나의 벡터로 만드는 작업을 수행하며, 이를 로 정의합니다. 는 예측 연산의 입력으로 사용하여 인코더로부터 얻은 정보를 활용해 를 좀 더 잘 예측할 수 있게 한다.
5) 출력층 연산의 입력인
어텐션 매커니즘에선 위에서 구한 를 바로 출력층으로 보내지 않고 그 전에 신경망 연산을 추가. 가중치 행렬과 곱한 후 하이퍼볼릭탄젠트 함수를 지나도록 하여 출력층 연산을 위한 새로운 벡터인 를 얻을 수 있다.
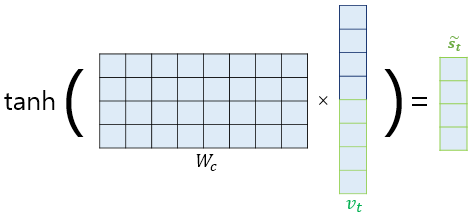
식으로 표현하자면 아래와 같다.

이때 가중치 행렬 의 크기는 (4, 8), 즉 위에서 설정한 (은닉 상태 크기, 은닉 상태 크기 x 2)이다. vt의 크기가 연결을 통해 (은닉 상태 크기 x 2, 1)이 되었기 때문이다. 어텐션을 소개한 논문에서는 위의 과정이 아래와 같은 수식으로 표현되었다.
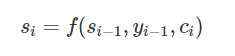
si: i번째 시점의 은닉 상태
yi−1: i-1번째 타겟 단어(or 예측 단어)
ci: i번째 시점의 컨텍스트 벡터
마지막으로 를 출력층의 입력으로 사용하여 예측 벡터를 계산한 후 소프트맥스를 적용하면 다음 예측 단어를 추론할 수 있다.
yt^=Softmax(Wyst~+by)
위의 과정을 한눈에 이해할 수 있는 어텐션 메커니즘을 정말 잘 그린 도식

출처: [Pytorch] 차근차근 구현하는 seq2seq + attention mechanism (tistory.com)
어텐션의 종류는 다양하다. 어텐션 차이는 중간 수식인 어텐션 스코어 함수 차이를 말하는데, 위에서 살펴본 것은 내적을 사용한 닷-프로덕트 어텐션이었다.

참조
딥 러닝을 이용한 자연어 처리 입문(https://wikidocs.net/22893)
https://moondol-ai.tistory.com/316?category=947304
'스터디 > 딥러닝' 카테고리의 다른 글
| Chapter1. 한눈에 보는 머신러닝 (0) | 2022.07.20 |
|---|---|
| [논문] ViT(Vision Transformer) (0) | 2022.07.18 |
| CNN VS FC (0) | 2022.07.14 |
| Pytorch vs Tensorflow (0) | 2022.03.15 |
| CNN-based Approaches For Cross-Subject Classification in Motor Imagery: From The State-of-The-Art to DynamicNet (0) | 2022.03.12 |



