18.6 정책 그래디언트 (PG, Policy Gradient)
정책 탐색에서 간단하게 살펴 보았듯이 정책 그래디언트(PG)는 높은 보상을 얻는 방향의 그래디언트로 정책(policy)의 파라미터를 최적화하는 알고리즘이다.
PG 알고리즘 중 인기있는 알고리즘은 1992년 로날드 윌리엄스(Ronald Williams)가 제안한 REINFORCE 알고리즘이다.
REINFORCE의 방법은 다음과 같다.
- 신경망 정책이 여러 번에 걸쳐 게임을 플레이하고 매 스텝마다 선택된 행동이 더 높은 가능성을 가지도록 만드는 그래디언트를 계산한다.
- 몇 번의 에피소드를 실행한 다음, 각 행동의 점수를 계산한다.
- 한 행동 점수가 양수이면 선택될 가능성이 높도록 1번에서 계산한 그래디언트를 적용한다. 만약, 음수일 경우 덜 선택 되도록 반대의 그래디언트를 적용한다.
- 그래디언트 벡터와 행동 점수를 곱해주면 된다.
- 마지막으로 모든 결과 그래디언트 벡터의 평균을 구한 다음 경사 하강법을 수행한다.
알고리즘 구현
카트 위의 막대가 균형 잡는 법을 학습하기 위해 만든 신경 정책 훈련
def play_one_step(env, obs, model, loss_fn):
with tf.GradientTape() as tape:
left_proba = model(obs[np.newaxis])
action = (tf.random.uniform([1, 1]) > left_proba)
y_target = tf.constant([[1.]]) - tf.cast(action, tf.float32)
loss = tf.reduce_mean(loss_fn(y_target, left_proba))
grads = tape.gradient(loss, model.trainable_variables)
obs, reward, done, info = env.step(int(action[0, 0].numpy()))
return obs, reward, done, grads- 만약 left_proba가 높다면, 동작은 False가 될 가능성이 높다.
- False는 숫자 캐스팅 시 0을 의미하므로 y_target은 1 - 0 = 1과 같다.
=>다시 말해, 우리는 목표를 1로 설정하는데, 이것은 왼쪽으로 갈 확률이 100%였어야 한다는 것을 의미한다.
- 주어진 손실 함수를 사용해 손실을 계산, 테이프를 사용해 모델의 훈련 가능한 변수에 대한 손실 그레디언트 계산
- 선택한 행동 플레이 후 새로운 관측, 보상, 에피소드 종료 여부, 계산한 그레이디언트 반환
play_one_step() 을 활용해 여러 에피소드 플레이, 전체 보상과 각 에피소드, 스텝의 그레디언트반환 함수
def play_multiple_episodes(env, n_episodes, n_max_steps, model, loss_fn):
all_rewards = []
all_grads = []
for episode in range(n_episodes):
current_rewards = []
current_grads = []
obs = env.reset()
for step in range(n_max_steps):
obs, reward, done, grads = play_one_step(env, obs, model, loss_fn)
current_rewards.append(reward)
current_grads.append(grads)
if done:
break
all_rewards.append(current_rewards)
all_grads.append(current_grads)
return all_rewards, all_grads이 코드는 보상 리스트의 리스트, 그레이디언트 리스트의 리스트를 반환한다.
정책 그레이디언트 알고리즘은 모델을 사용하여 에피소드를 여러 번(예: 10회) 재생한 다음 다시 돌아가서 모든 보상을 살펴보고 할인하고 정규화하는 함수 만들기위해 함수 몇 개가 더 필요하다.
- 첫 번째 기능은 할인된 보상을 계산할 것이고, 두 번째 기능은 많은 에피소드에 걸쳐 할인된 보상을 정상화할 것 이다.
# 각 스텝에서 할인된 미래 보상의 합을 계산
def discount_rewards(rewards, discount_rate):
discounted = np.array(rewards)
for step in range(len(rewards) - 2, -1, -1):
discounted[step] += discounted[step + 1] * discount_rate
return discounted
# 여러 에피소드에 걸쳐 계산된 할인된이 모든 보상에서 평균을 빼고 표준편차를 나누어 정규화
def discount_and_normalize_rewards(all_rewards, discount_rate):
all_discounted_rewards = [discount_rewards(rewards, discount_rate)
for rewards in all_rewards]
flat_rewards = np.concatenate(all_discounted_rewards)
reward_mean = flat_rewards.mean()
reward_std = flat_rewards.std()
return [(discounted_rewards - reward_mean) / reward_std
for discounted_rewards in all_discounted_rewards]
하이퍼 파라미터 정의
n_iterations = 150
n_episodes_per_update = 10
n_max_steps = 200
discount_rate = 0.95- 훈련 반복 150번
- 각 반복은 에피소드 10개를 실행
- 각 에피소드는 스텝을 최대 200번 플레이
- 할인 계수 0.95적용
옵티마이저와 손실함수
optimizer = keras.optimizers.Adam(learning_rate=0.01)
loss_fn = keras.losses.binary_crossentropy # 이진분류기 훈련
훈련반복
for iteration in range(n_iterations):
all_rewards, all_grads = play_multiple_episodes(
env, n_episodes_per_update, n_max_steps, model, loss_fn)
total_rewards = sum(map(sum, all_rewards)) # Not shown in the book
print("\rIteration: {}, mean rewards: {:.1f}".format( # Not shown
iteration, total_rewards / n_episodes_per_update), end="") # Not shown
all_final_rewards = discount_and_normalize_rewards(all_rewards,
discount_rate)
all_mean_grads = []
for var_index in range(len(model.trainable_variables)):
mean_grads = tf.reduce_mean(
[final_reward * all_grads[episode_index][step][var_index]
for episode_index, final_rewards in enumerate(all_final_rewards)
for step, final_reward in enumerate(final_rewards)], axis=0)
all_mean_grads.append(mean_grads)
optimizer.apply_gradients(zip(all_mean_grads, model.trainable_variables))
하지만 더 크고 복잡한 문제는 잘 적용되지 못한다...
18.7 마르코프 결정 과정
20세기 초 수학자 Andrey Markov는 메모리가 없는 확률 과정(stochastic process)인 마르코프 체인(Markov Chain)에 대해 연구했다. 이 과정은 정해진 개수의 상태(state)를 가지고 있으며, 각 스텝마다 한 상태에서 다른 상태로 랜덤하게 전이된다.
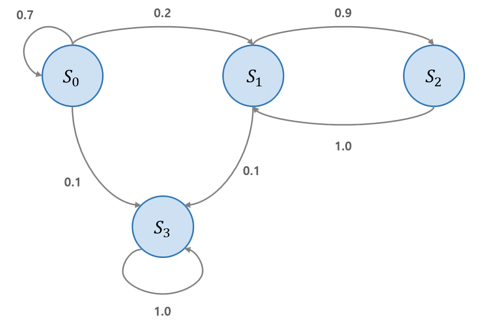
마르코프 성질
: 상태 s 에서 s'로 전이 하기 위한 확률은 고정, 메모리가 없기 때문에 과거 상태에 상관없이 (s,s')쌍에만 의존한다.
위의 그림 설명
- 상태 S0에서 시작한다고 했을 때, 다음 스텝에서 S0에 있을 확률은 0.7이다.
- 0.2의 확률로 S1로 전이됐을 경우 S2로 전이될 확률이 0.9이기 때문에 S2로 갈 가능성이 높다.
- S2로 갔을 경우 1.0의 확률로 다시 S1로 돌아오게 된다.
-만약, 0.1의 확률로 S3으로 전이 된다면, 영원히 S3에 남게되는데, 이 상태를 종료 상태(terminal state)라고 한다.
마르코프 결정 과정(MDP, Markov Decision Process)
1950년대 Richard Bellman에 의해 처음 사용되었다. 마코프 체인과 비슷하지만 MDP는 다음과 같은 특징을 가진다.
- 각 스텝에서 에이전트(agent)는 여러 가능한 행동(action) 중 하나를 선택할 수 있다.
- 전이 확률은 선택된 행동에 따라 달라지며, 어떤 상태로의 전이는 보상(reward)을 반환한다.
- 그리고 에이전트의 목적은 시간이 지남에 따라 보상을 최대화하기 위한 정책을 찾는 것이다.
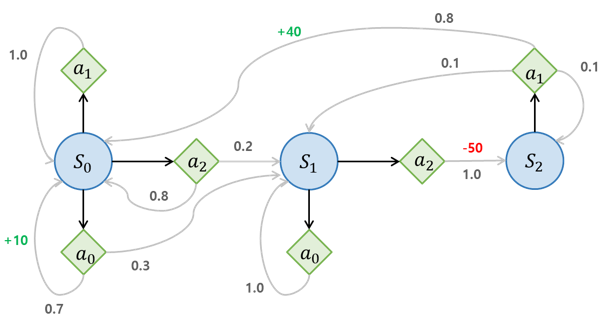

벨먼 최적 방정식
어떤 상태 s의 최적 상태 가치를 추정하는 방법
에이전트가 최적으로 행동하면 현재 상태의 최적 가치는 하나의 최적 행동으로 인해 평균적으로 받게 될 보상과 이 행동이 유발할 수 있는 가능한 모든 다음 상태의 최적 가치릐 기대치를 합한 것과 같다.

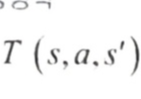
: 에이전트가 a를 선택했을때 상태 s에서 s'로 전이될 확률 => 전이 확률

: 에이전트가 a를 선택해서 상태 s에서 s'로 이동됐을때 받을 수 있는 보상 => 보상
이 식은 최적의상태 가치를정확이 추정할 수 있도록 도와준다.
- 모든 상태 가치를 0으로 초기화하고 가치반복 알고리즘을 사용해 반복적으로 업데이터 하면 최적의 상태 가치에 수렴하는 것이 보장된다.
참고



