18.8 시간차(Temporal Difference) 학습
독립적인 행동으로 이루어진 강화학습 문제는 보통 마르코프 결정 과정으로 모델링될 수 있지만 학습 초기에 에이전트는 전이 확률( T(s,a,s') )에 대해 알지 못하며, 보상( R(s,a,s') )이 얼마나 되는지 알지 못한다. 그렇기 때문에, 보상에 대해 알기 위해서는 적어도 한번씩은 각 상태(state)와 전이를 경험해야 하며, 전이 확률에 대해 신뢰할만한 추정을 얻기 위해서는 여러번 경험을 해야한다.
시간차 학습(TD 학습, Temporal Difference Learning)은 가치 반복(Value-iteration) 알고리즘과 비슷하지만,
1. 에이전트가 MDP에 대해 일부의 정보만 알고 있을 때 다룰 수 있도록 변형한 것
2. 일반적으로 에이전트가 초기에 가능한 상태와 행동만 알고 있다고 가정
에이전트는 탐험 정책(exploration policy)을 사용해 MDP를 탐험하고, TD 학습 알고리즘이 관측된 전이와 보상에 근거하여 업데이터 하는 방식이다.

α : 학습률(learning rate)
18.9 Q-Learning
모든 상태에서 취하는 각각의 행동에 대해 보상을 얼마나 받을지 미리 알고 있다고 가정했을 때 행동을 어떻게 결정하면 될까?
최종적으로 가장 높은 보상을 받을 수 있는 행동들을 연속적으로 취하면 된다!
이렇게 최종적으로 받는 모든 보상의 총합을 Q-value (Quality Value) 라고 한다.
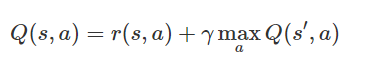
Q(s,a) : 상태 s 에서 행동 a 를 취할 때 받을 수 있는 모든 보상의 총합
(현재 행동을 취해서 받을 수 있는 즉각보상과 미래에 받을 미래보상의 최대값의 합)
r(s,a) : 현재 상태 s 에서 행동 a 를 취했을 때 받을 즉각보상값
s′ : 은 현재 상태 s 에서 행동 a 를 취해 도달하는 바로 다음의 상태
maxQ(s′,a) : 다음 상태 s′에서 받을 수 있는 보상의 최대값
γ : 할인율이라고 부르는 값으로, 미래가치에 대한 중요도를 조절
Agent의 목표는 이 값을 최대화 할 수 있는 행동을 선택해내는 것
Q-Learning은 전이 확률과 보상을 초기에 알지 못하는 상황에서 Q-가치 반복 (Q-value Iteration) 알고리즘을 적용한 것이다.
"어떤 상태이든, 가장 높은 누적 보상을 얻을 수 있는 행동을 취한다"
매 순간 가장 높다고 판단되는 행동을 취한다는 점에서, 이 알고리즘은 greedy (탐욕적) 이다.
이런 전략을 현실 문제에는 어떻게 적용시킬 수 있을까?
- 모든 가능한 상태-행동 조합을 표로 그리고, 거기에 모든 Q-value를 적어 사용
- 그 후에는 벨만 방정식을 이용해서 표를 점점 업데이트하는 방법

Agent가 가장 오른쪽 위 칸에 도달하면 끝나는 게임
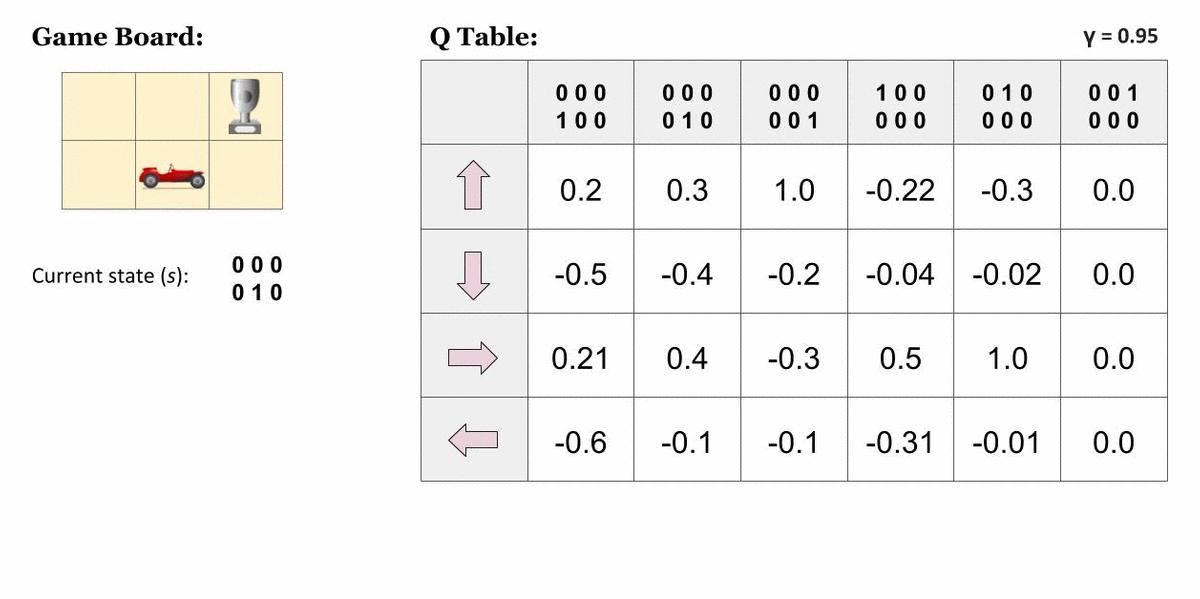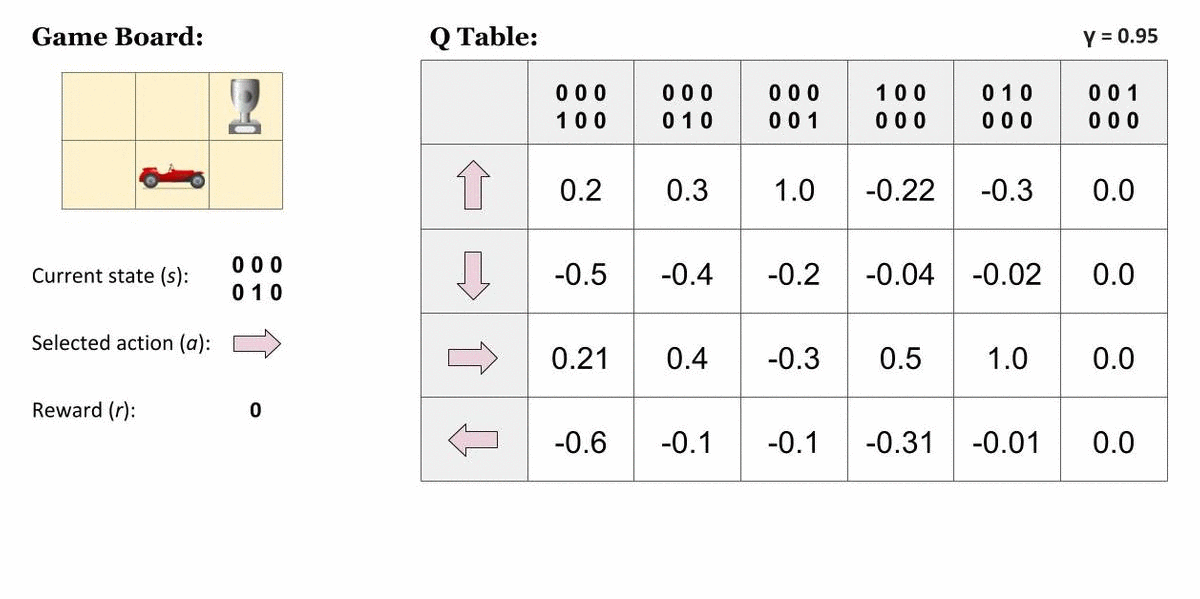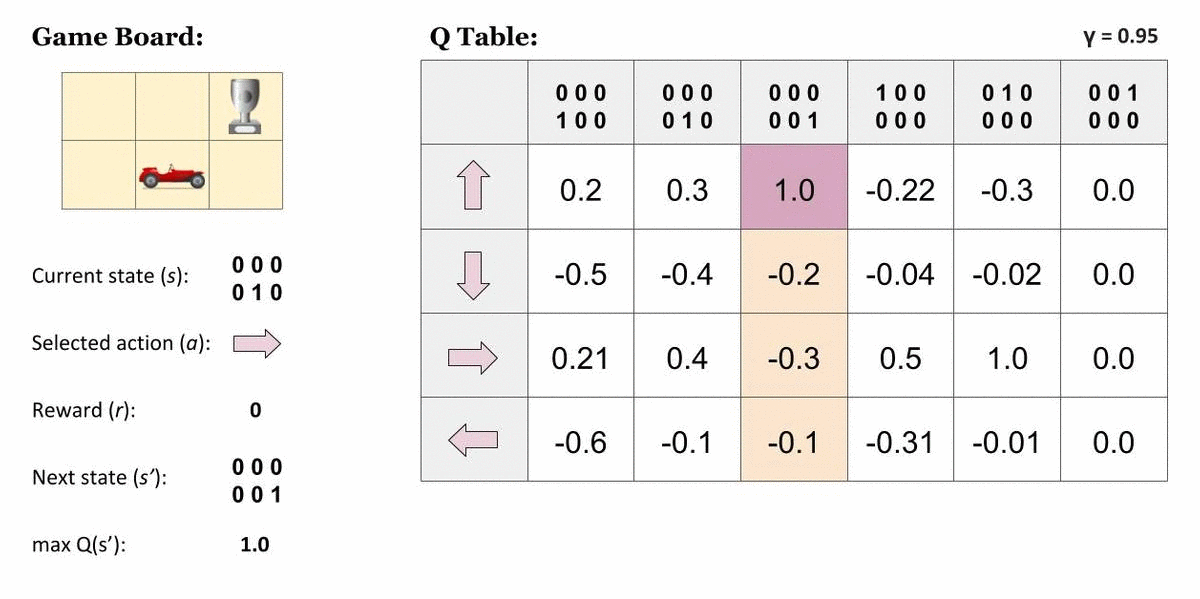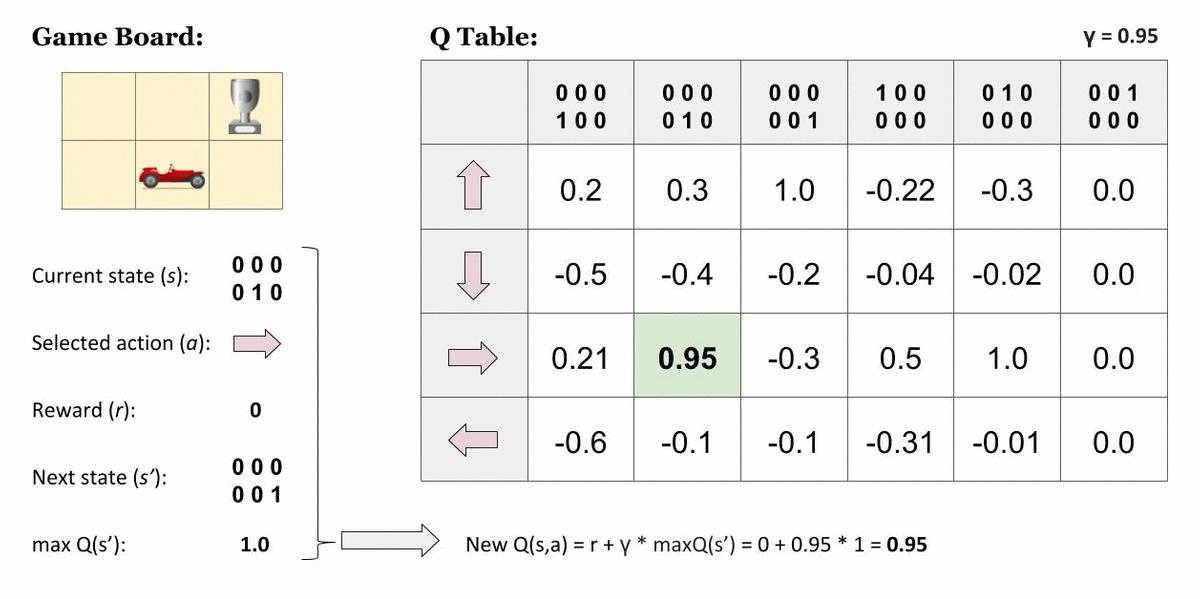
표에서 맨 오른쪽 열이 나타내는 상태는 종결상태입니다. 이 상태에서 Agent는 아무런 행동 또는 상태 변화를 할 수 없기 때문에 모든 값은 0입니다. 그렇다면, 종결상태인 s′에 도달하기 직전의 상태에 대해서는 이렇게 단순히 그 다음 순간 받을 즉각 보상으로만 가치를 산정할 수 있을 것입니다.
탐욕적 알고리즘의 문제점
만약 항상 '최선의 선택'만 고집한다면, 새로운 선택은 해보지 않을 것이고, 그렇게 된다면 아직 받아보지 못한 미지의 보상에 대해서는 앞으로도 그 존재를 알 수 없다.
8.9.1 탐험 정책
탐험 정책(exploration policy)를 사용해 MDP를 탐험해야 Q-Learning이 동작한다. 이때 탐험 정책이 랜덤하게 이루어 진다면, 운이 나쁜 경우 매우 오랜 시간이 걸릴 수 있다. 랜덤한 방법 보다 더 나은 방법으로는 ϵ-greedy policy를 사용하는 것이다.
ϵ-greedy policy
- 0<ϵ<1 인 어떤 ϵ 값을 이용해서, 탐험과 활용을 적절히 번갈아가며 사용
- 각 스텝에서 ϵ 의 확률로 랜덤하게 행동
- 1−ϵ의 확률로는 원래 했던 대로 탐욕적으로 행동을 선택 (1- ϵ의확률로 그 순간 가장 높은 Q-value를 선택해 행동)
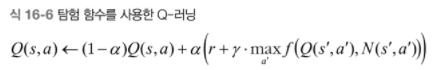
- N(s', a') : 상태 s'에서 행동 a'를 선택한 횟수
8.9.2 Deep Q-Network (DQN)
Q-Learning의 가장 치명적인 문제는 대규모의 상태와 행동을 가진 MDP에는 적용하기 어렵다는 것이다.
이러한 문제를 해결하기위해 Q-value를 추정하기 위해 사용하는 DNN인 DQN을 사용할 수 있다.
DQN을 훈련시키기 위해서는 타겟값이 필요한데, 타겟값은 다음과 같이 구할 수 있다.
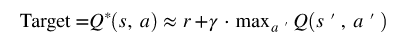
위의 타겟 Q-value와 추정된 Q-value의 제곱 오차를 최소화하는 방향으로 훈련시킬 수 있다.

딥마인트가 제안한 DQN 알고리즘
- Replay memory에 경험 데이터를 저장하여, 각 반복마다 훈련 배치를 랜덤하게 샘플링해준다. 이렇게 해줌으로써 훈련 배치의 겨엄 데이터 사이에 있는 상관관계(correlation)을 감소시켜 훈련 성능을 높인다.
- 딥마인드의 DQN은 두 개의 DQN을 사용한다.
- Online DQN : 훈련 반복마다 플레이하고 학습한다.
- Target DQN : 타겟 Q-value를 계산할 때만 사용된다. 일정한 간격으로 Online-DQN의 가중치가 Target DQN으로 복사된다.
- 두 개의 네트워크를 구성함으로써 훈련 과정을 안정화시키는 데 도움을 준다.
참고
'스터디 > 딥러닝' 카테고리의 다른 글
| Pytorch vs Tensorflow (0) | 2022.03.15 |
|---|---|
| CNN-based Approaches For Cross-Subject Classification in Motor Imagery: From The State-of-The-Art to DynamicNet (0) | 2022.03.12 |
| 핸즈온 머신러닝(Hands-On Machine Learning) 18장 - 강화학습(2) (0) | 2021.10.30 |
| 핸즈온 머신러닝(Hands-On Machine Learning) 18장 - 강화학습(1) (0) | 2021.10.28 |
| 핸즈온 머신러닝(Hands-On Machine Learning) 10장 - 케라스를 사용한 인공 신경망 (2)-1 (0) | 2021.10.27 |



